X 2 Y 2 Identity
gruposolpac
Sep 10, 2025 · 6 min read
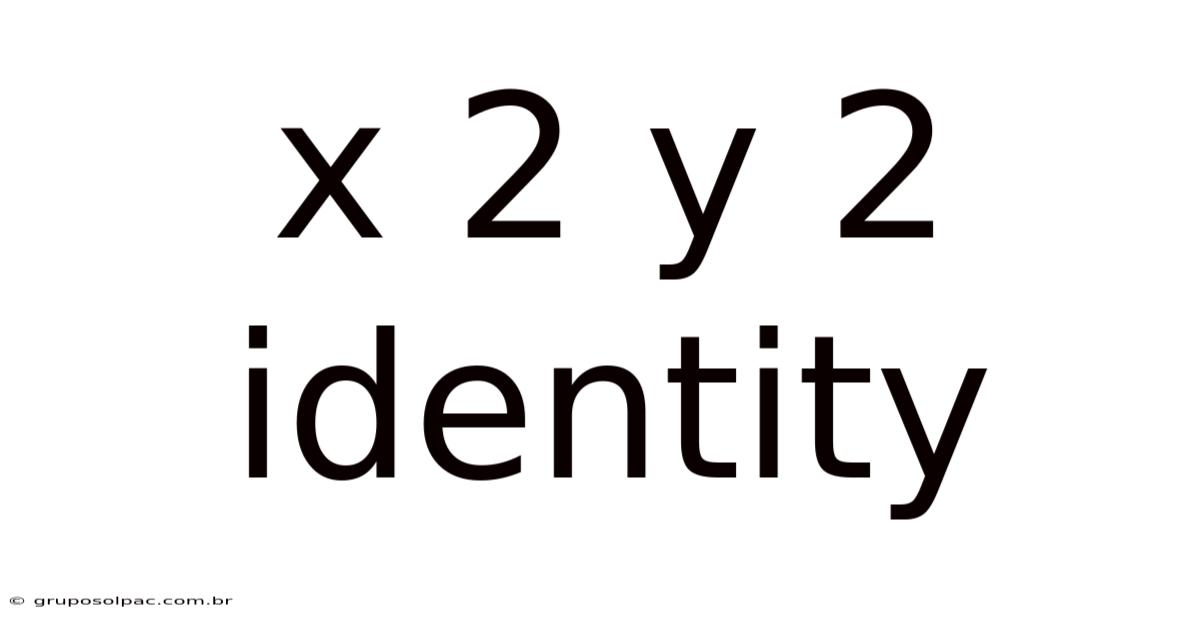
Table of Contents
Unraveling the X² - Y² Identity: A Deep Dive into Algebraic Factorization
The expression x² - y² is a fundamental concept in algebra, representing the difference of two squares. Understanding and mastering its factorization – the x² - y² identity – is crucial for simplifying algebraic expressions, solving equations, and tackling more advanced mathematical concepts. This article provides a comprehensive exploration of the x² - y² identity, encompassing its derivation, applications, and extensions, ensuring a thorough understanding for learners of all levels.
Introduction: What is the X² - Y² Identity?
The x² - y² identity, also known as the difference of squares factorization, states that the difference of two perfect squares can be factored into the product of their sum and difference. Mathematically, this is represented as:
x² - y² = (x + y)(x - y)
This seemingly simple equation forms the cornerstone of numerous algebraic manipulations and is a key tool for simplifying complex expressions. We'll explore how this identity works, why it's true, and its numerous applications in various mathematical contexts.
Deriving the X² - Y² Identity: A Step-by-Step Approach
The identity isn't just a statement; it's a direct consequence of the distributive property of multiplication. Let's derive it step-by-step:
-
Start with the right-hand side: We begin with the factored form: (x + y)(x - y).
-
Apply the distributive property (FOIL method): Multiply each term in the first parenthesis by each term in the second parenthesis. This gives us:
x(x - y) + y(x - y)
-
Distribute further: This expands to:
x² - xy + xy - y²
-
Simplify: Notice that the terms -xy and +xy cancel each other out. This leaves us with:
x² - y²
This demonstrates that (x + y)(x - y) is indeed equivalent to x² - y², proving the identity.
Understanding the Geometry Behind the Identity
The x² - y² identity also has a fascinating geometric interpretation. Imagine a large square with side length x and a smaller square with side length y cut out from one corner. The area of the large square is x², and the area of the smaller square is y². The remaining area represents the difference, x² - y².
Now, consider rearranging the remaining pieces. You can create a rectangle with dimensions (x + y) and (x - y). The area of this rectangle is (x + y)(x - y). Since the area remains unchanged after rearrangement, this visually confirms that x² - y² = (x + y)(x - y). This geometrical representation makes the abstract algebraic concept more intuitive and easier to grasp.
Applications of the X² - Y² Identity: Solving Equations and Simplifying Expressions
The x² - y² identity is a powerful tool with widespread applications in various areas of mathematics:
-
Factoring Quadratic Expressions: Many quadratic expressions can be simplified using this identity. For instance, consider 4x² - 9. We can rewrite this as (2x)² - (3)², directly applying the identity to obtain (2x + 3)(2x - 3).
-
Simplifying Algebraic Fractions: The identity helps simplify fractions. For example, (x² - 16) / (x - 4) can be factored as [(x + 4)(x - 4)] / (x - 4). If x ≠ 4, we can cancel out the (x - 4) terms, simplifying the fraction to (x + 4).
-
Solving Quadratic Equations: The identity plays a crucial role in solving quadratic equations. For instance, in the equation x² - 25 = 0, we can factor it as (x + 5)(x - 5) = 0, leading to solutions x = 5 and x = -5.
-
Calculus: This identity often simplifies calculations involving derivatives and integrals, particularly when dealing with expressions containing differences of squares.
-
Number Theory: The difference of squares identity has important applications in number theory, aiding in the factorization of numbers and the study of prime numbers.
Extending the X² - Y² Identity: Exploring Variations and Generalizations
While the basic identity is straightforward, its principles can be extended to more complex scenarios:
-
Difference of Higher Powers: Although not a direct extension, understanding the difference of squares lays the groundwork for factoring differences of higher even powers. For example, x⁴ - y⁴ can be factored as (x² + y²)(x² - y²), and the second term can be further factored using the difference of squares identity.
-
Sum and Difference of Cubes: While not directly related, the methods used to derive the difference of squares identity are analogous to deriving the sum and difference of cubes identities:
- x³ + y³ = (x + y)(x² - xy + y²)
- x³ - y³ = (x - y)(x² + xy + y²)
These identities, while distinct, demonstrate the power of factoring and its application to various polynomial forms.
Common Mistakes and How to Avoid Them
While seemingly simple, several common mistakes can arise when using the x² - y² identity:
-
Incorrect Identification of Perfect Squares: Ensure both terms are perfect squares before applying the identity. For example, x² - 2y is not a difference of squares because 2y is not a perfect square.
-
Incorrect Sign in the Factored Form: Remember the factored form is (x + y)(x - y), with one factor being a sum and the other a difference. Getting the signs wrong leads to an incorrect factorization.
-
Forgetting to Check for Common Factors: Before applying the difference of squares identity, always check for common factors that can be factored out first. This simplifies the expression and makes the application of the identity easier.
Frequently Asked Questions (FAQ)
Q1: Can the x² + y² identity be factored?
A1: No, x² + y² (the sum of two squares) cannot be factored using real numbers. It can be factored using complex numbers, resulting in (x + iy)(x - iy), where 'i' is the imaginary unit (√-1).
Q2: What if x and y are not integers?
A2: The x² - y² identity holds true even if x and y are not integers, provided they are real numbers. The identity works for rational numbers, irrational numbers, and even variables representing real numbers.
Q3: How can I apply this identity to solve word problems?
A3: Word problems often involve geometric areas or quantities that can be represented by quadratic expressions. By recognizing the difference of squares, you can translate a word problem into an algebraic equation solvable using the identity.
Q4: Are there any limitations to the x² - y² identity?
A4: The primary limitation is the requirement that both terms are perfect squares. Also, remember to always check for common factors before applying the identity.
Conclusion: Mastering the X² - Y² Identity – A Foundation for Algebraic Success
The x² - y² identity, although seemingly simple at first glance, is a fundamental concept with far-reaching implications in algebra and beyond. Mastering this identity is not merely about memorizing a formula; it's about understanding its derivation, its geometric interpretation, and its wide range of applications in simplifying expressions, solving equations, and tackling more advanced mathematical concepts. By understanding its principles and avoiding common pitfalls, you'll build a solid foundation for success in algebra and related fields. The ability to recognize and apply the x² - y² identity efficiently is a key skill that will serve you well throughout your mathematical journey. Remember to practice regularly and explore various examples to truly internalize this powerful algebraic tool.
Latest Posts
Latest Posts
-
Relation Between Power And Velocity
Sep 10, 2025
-
Explain The Term Inductive Reactance
Sep 10, 2025
-
Miscellaneous Expenses In Final Accounts
Sep 10, 2025
-
State And Prove Stokes Law
Sep 10, 2025
-
Advantages Of Cost Accounting Pdf
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 Identity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.